Extension Springs
Pegas ekstensi menyerap dan menyimpan energi serta menciptakan resistensi terhadap gaya tarik. Pegas ini biasanya terpasang di kedua ujungnya ke komponen lain dan ketika komponen ini bergerak terpisah, pegas mencoba menyatukannya kembali. Ini adalah tegangan awal yang menentukan seberapa erat pegas digulung. Tegangan awal ini dapat dimanipulasi untuk mencapai persyaratan beban aplikasi tertentu. Desain biasanya memiliki kait, mata, atau geometri antarmuka lainnya di ujungnya yang menempel pada komponen yang berlawanan. Pegas ini sering digunakan untuk memberikan gaya balik ke komponen yang memanjang dalam posisi yang digerakkan.
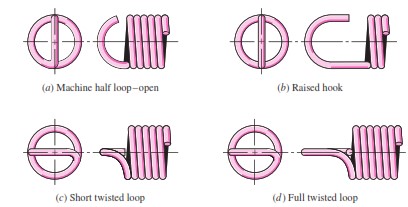

Tegangan di badan pegas ekstensi ditangani sama seperti kompresi mata air. Dalam merancang pegas dengan ujung kait, tekukan dan puntiran pada kait harus disertakan dalam analisis. Pada Gambar 2a dan 2b metode yang umum digunakan untuk merancang tampilan akhir. Tegangan tarik maksimum di A, karena torsi dan pembebanan aksial, dirumuskan menjadi
σA = F {(K)A [(16D/πd3) + (4/πd2)]}
di mana (K)A adalah faktor koreksi tegangan bending untuk kelengkungan, yang dirumuskan
(K)A = [4C12-C1-1] / [4C1(C1-1)] ; C1 = 2r1/d
Tegangan torsi maksimal pada titik B yaitu
τB = (K)B (8FD/πd3)
di mana faktor koreksi tegangan untuk kelengkungan, (K)B, adalah
(K)B = [4C2-1] / [4C2-4)] ; C2 = 2r2/d
Gambar 2c dan 2d menunjukkan desain yang ditingkatkan karena diameter kumparan yang berkurang.

tegangan torsi akibat tegangan awal sebagai fungsi dari indeks pegas C dalam pegas ekstensi.
Ketika pegas ekstensi dibuat dengan kumparan yang bersentuhan satu sama lain, hal ini disebut sebagai close-wound. Pabrikan pegas lebih menyukai ketegangan awal dalam pegas close-wound untuk menahan panjang bebas lebih akurat. Defleksi beban yang sesuai kurva ditunjukkan pada gambar 3a, di mana y adalah perpanjangan di luar panjang bebas. L0 dan Fi adalah tegangan awal pegas yang harus dilampaui sebelum pegas cacat. Hubungan beban-defleksi adalah
F =Fi + ky
dimana k adalah konstanta pegas. Panjang bebas L0 pegas diukur di dalam ujungnya loop atau kait seperti yang ditunjukkan pada Gambar 3b dapat dinyatakan sebagai:
L0 = 2(D-d) + (Nb+1)d = (2C-1+Nb)d
di mana D adalah diameter kumparan rata-rata, Nb adalah jumlah kumparan tubuh pegas, dan C adalah indeks pegas. Dengan loop ujung bengkok biasa seperti yang ditunjukkan pada Gambar 3b, untuk memperhitungkan defleksi loop dalam menentukan laju pegas k, jumlah ekivalen dari heliks aktif adalah Na yang dirumuskan menjadi
Na = Nb + G/E
di mana G dan E adalah modulus elastisitas geser dan tarik.
Jumlah tegangan awal yang dapat dipakai oleh perancang pegas secara rutin adalah seperti yang ditunjukkan pada Gambar 3c. Rentang pilihan tersebut dapat dinyatakan dengan tegangan torsi tidak terkoreksi τi
τi = [33 500 /exp(0.105C)] ± 1000 [4-(c-3)/6.5] ; C adalah indeks pegas
>>> KLIK DI SINI UNTUK MEMBACA ARTIKEL TENTANG ELEMEN MESIN LAINNYA!
Kontributor : Daris Arsyada
Sumber:
Budynas, Richard G dan J. Keith Nisbett. 2011. Shigley’s Mechanical Engineering Design: Ninth Edition. Amerika Serikat: The McGraw-Hill Companies, Inc.


Leave a Reply
Want to join the discussion?Feel free to contribute!