Contoh Soal Beban Statis pada Pengelasan (Welding)
Beberapa contoh sambungan yang dibebani secara statis berguna dalam membandingkan dan mengontraskan metode analisis konvensional dan metodologi kode pengelasan. Di bawah ini adalah beberapa contoh soal beban statis pengelasan.
Contoh 1

Sebuah batang 1/2 in di dalam penampang logam batang persegi panjang 1015 2-in membawa beban statis 16,5 kip. Bar dilas ke pelat buhul dengan las fillet 3/8 in pada di kedua sisi dengan E70XX elektroda seperti yang digambarkan pada Gambar 1. Gunakan metode kode pengelasan.
a) Apakah kekuatan logam las memuaskan?
b) Apakah sambungan lasnya memuaskan?
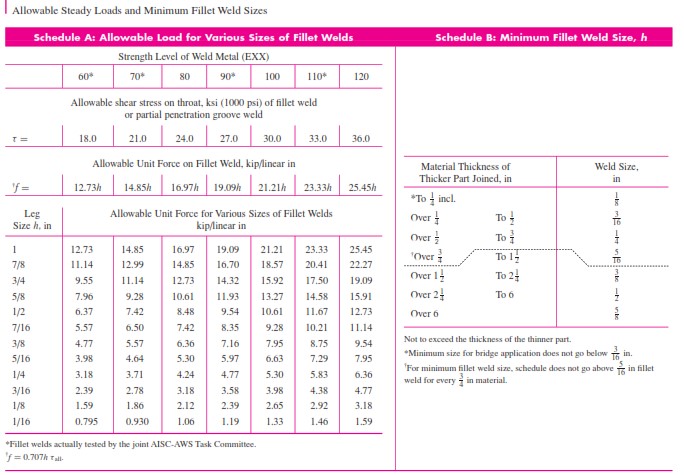
a) Dari Tabel 1, gaya yang diijinkan per satuan panjang untuk logam elektroda E70 3/8 in adalah 5,57 kip/in dari pengelasan; jadi
F= 5.57l = 5.57(4)= 22.28 kip
Karena 22,28 > 16,5 kip, kekuatan logam las cukup memuaskan.
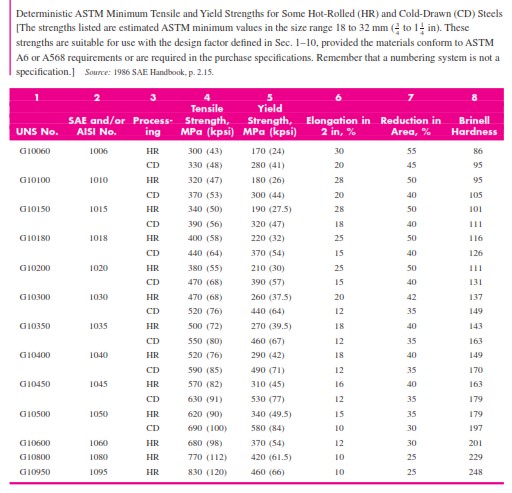
b) Periksa gaya geser pada sambungan yang berdekatan dengan lasan. Dari Tabel ASTM hot-rolled dan cold-drawn Sy 27,5kpsi. = Kemudian, dari Tabel 2, tegangan geser perlekatan yang diijinkan adalah
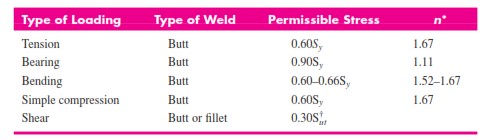
τall 0.4Sy = 0.4(27.5) = 11 kpsi
Tegangan geser τ pada logam dasar yang berdekatan dengan lasan adalah
τ = F/(2hl) = 16.5/(2*0.375*2) = 11 kpsi
karena τall <= τ, sambungan memuaskan di dekat las. Tegangan tarik dalam batang sambungan σ adalah
σ = F/tl = 16.5 kpsi
Tegangan tarik yang diijinkan σall dari Tabel 2, adalah 0,6Sy dan dengan tingkat keamanan kode pengelasan dipertahankan
σall = 0.6Sy = 0.6(27.5) = 16.5 kpsi
karena σ ≤ σall , kekuatan sambungan memuaskan.
Contoh 2
Ada sebuah kantilever las yang dibebani secara statis 500 lbf digambarkan pada Gambar 2. Kantilever terbuat dari baja AISI 1018 HR dan dilas dengan 3/8 in las fillet seperti yang ditunjukkan pada gambar. Elektroda E6010 digunakan, dan faktor desain adalah 3.0.
a) Gunakan metode konvensional untuk logam las.
b) Gunakan metode konvensional untuk logam pengikat (kantilever).
c) Gunakan kode las untuk logam las.
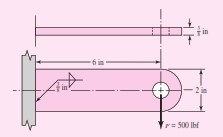

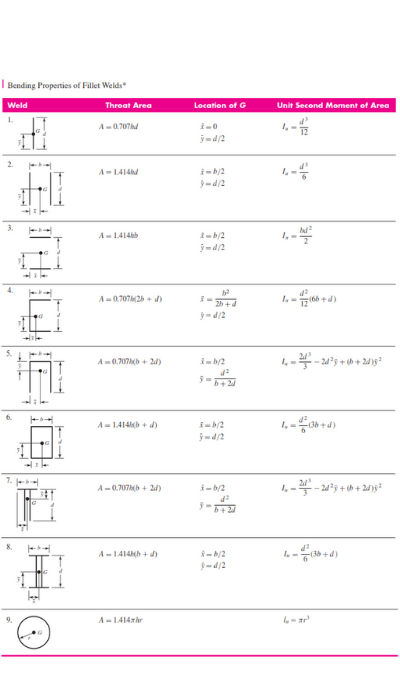
a) dari tabel 3 Sy = 50 kpsi, Sut = 62 kpsi, dari tabel 4 pola kedua, b= 0.375 in, d = 2 in, jadi
A = 1.414hd = 1.414(0.375)2 = 1.06 in2
Iu = d3/6 = 23/6 = 1.33 in
I = 0.707hIu = 0.707 (0.375) 1.33 = 0.353 in4
Gaya geser primer τ’ = F/A = 500 (10-3) / 1.06 = 0.472 kpsi
Gaya geser sekunder τ” = Mr/I = 500 (10-3) (6) (1) / 0.353 = 8.50 kpsi
Besar gaya geser τ adalah kombinasi Pythagoras τ = (τ’2 + τ”2)1/2 = (0.4722 + 8.502)1/2 = 8.51 kpsi
Faktor keamanan berdasarkan kekuatan minimum dan kriteria energi distorsi adalah
n = Ssy / τ = 0.557 (50) / 8.51 = 3.39
Karena n ≥ nd ; 3.39 ≥ 3.0 logam las memiliki kekuatan yang cukup
b) Dari tabel ASTM: Gaya tarik minimal dan kekuatan yield pada baja hot-rolled dan cold-drawn, kekuatan minimal Sut = 58 kpsi dan Sy = 32 kpsi, lalu
σ = M / (I/c) = M/ (bd2/6) = 500 (10-3) 6 / (0.375*22 / 6) = 12 kpsi
n = Sy / σ = 32/12 = 2.67
karena n < nd, kekuatan sambungan pada logam pengikat tidak cukup
c) Dari bagian (a), τ = 8,51 kpsi. Untuk elektroda E6010 pada Tabel 1 tegangan geser yang diizinkan τall adalah 18 kpsi. Karena τ < τall, pengelasannya memuaskan. Karena kodenya sudah memiliki faktor desain 0,577(50)/18 = 1.6 termasuk pada kesetaraan, yang sesuai faktor keamanan pada bagian (a) adalah
n = 1.6 (18/8.51) = 3.38 -> konsisten
>>> KLIK DI SINI UNTUK MEMBACA ARTIKEL TENTANG ELEMEN MESIN LAINNYA!
Kontributor : Daris Arsyada
Sumber:
Budynas, Richard G dan J. Keith Nisbett. 2011. Shigley’s Mechanical Engineering Design: Ninth Edition. Amerika Serikat: The McGraw-Hill Companies, Inc.



Leave a Reply
Want to join the discussion?Feel free to contribute!