Pada part ke 2 ini, akan dibahas lebih mendetail terkait permodelan material-material non-linear elastic, yang pada aplikasi dunia nyata sangatlah banyak ditemui, dan terkadang menghasilkan solusi yang sangat berbeda dibandingkan dengan permodelan menggunakan material yang linear.
Pada artikel ini, akan dibahas secara spesifik material nonlinear elastic (dapat kembali ke bentuk semula), untuk material dengan karakteristik damage, plastisitas, dan lain-lain akan dibahas pada part selanjutnya.
Sebelum membahas material-material non-linear elastic, berikut kita bahas secara singkat material linear terlebih dahulu:
Linear Elastic Material
Material isotropic yang memenuhi hukum Hooke linear.
Material jenis ini adalah yang paling populer untuk digunakan, terutama untuk simulasi pembebanan struktur baja atau metal lainya secara sederhana, karena sudah cukup mewakili kondisi real dari material-material tersebut yang sebagian besar adalah isotropic.
Model material ini didefinisikan dengan hubungan modulus elastisitas (E) dengan modulus geser (G) sebagai berikut:
G = E/2(1+nu)
dengan nu adalah poison ratio.
Kemudian, material ini disebut linear karena grafik antara beban atau stress terhadap deformasi atau strain nya berupa garis yang linear pada pengujian beban uniaxial:
Dari grafik di atas, dapat dilihat bahwa material ini sangatlah sederhana, sehingga proses komputasi menjadi sangat efisien dan dapat mencakup banyak sekali kasus. Namun perlu diingat juga, karena liniaritasnya, tegangan dan regangan dari material ini dapat mencapai nilai yang tidak terhingga; artinya, material ini tidak akan pernah gagal pada tegangan setinggi apapun dan deformasi yang sangat ekstrim sekalipun; yang tentu saja tidak valid dalam kondisi ekstrim tersebut, oleh karena itu permodelan material menjadi penting pada banyak kasus aplikasi dunia nyata.
Material Non-linear Elastic
Hypoelastic
Material hypoelastic adalah material yang mengalami sifat nonlinear meskipun pada strain yang sangat rendah.
Dalam mekanika kontinuum, material hypoelastic merupakan material elastis (dapat kembali ke bentuk semula) yang model konstitutif nya independen terhadap finite strain atau laju deformasi. Model ini berbeda dengan hyperelastic kecuali pada beberapa kondsi tertentu. Pada aplikasinya, salah satu contoh material yang dapat dimodelkan dengan permodelan hypoelastic adalah concrete.
Hyperelastic (Isotropic)
Model material Hyperelastic adalah material dengan sifat yang dideskripsikan dengan persamaan strain energy potential (strain energy per satuan volume), yang biasa digunakan untuk memodelkan material dengan strain yang sangat besar namun masih elastis, seperti rubber, solid propellant, atau material elastomer lainya.
Berikut adalah contoh kurva tegangan-regangan tipikal pada material elastomer:
Material elastomer pada umumnya bersifat incompressible, kemudian bulk modulusnya beberapa kali lipat lebih besar dari shear modulusnya. Pendekatan incompressible dapat dilakukan pada banyak kasus, namun untuk material seperti foam pendekatan compressible harus dilakukan.
Berikut adalah beberapa model pendekatan material hyperelastic:
Total Lagrangian Formulation
Strain diukur menggunakan persamaan Green-Lagrange strain sebagai berikut:
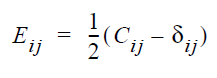
Dengan C adalah right Cauchy-Green deformation tensor.
Updated Lagrange Formulation
Pada formulasi ini, strain diukur menggunakan persamaan logaritmik sebagai berikut:

Dengn b adalah left Caucy-Green atau finger tensor.
Model Generalized Mooney-Rivlin (gmr)
Model generalisasi Mooney-Rivlin pada elastomer nearly-incompressible dituliskan dengan persamaan sebagai berikut:

Dengan I1 dan I2 adalah deviatoric invariant pertama dan kedua.
Model Jamus-Green-Simpson
Salah satu contoh khusus dari Mooney-Rivling model, yaitu third order deformation (tod) model. Meskipun demikian, Ogden (dijelaskan di bawah) masih lebih baik untuk strain yang besar bahkan untuk Mooney-Rivlin orde 5. Berikut adalah persamaan dari model tod:

Dengan nilai C adalah konstanta yang diperoleh dari hasil eksperimen.
Bentuk yang lebih populer dan lebih sederhana dari fungsi di atas adalah sebagai berikut:

Model Ogden
Bentuk persamaan dari model Ogden ini adalah sebagai berikut:

Dengan Lambda adalah deviatoric stretch ratio, sedangkan C, miu, dan alpha adalah hasil curve fitting dari hasil eksperimen.
Karena bentuk persamaan yang berbeda dengan Mooney-Rivlin, Model Ogden ini bisa diaplikasikan pada material yang sedikit kompresibel.
Model Arruda-Boyce
Dalam model Arruda-Boyce, struktur molekul dari material elastomer direpresentasikan dengan eight-chain model untuk mensimulasikan sifat non-Gaussian pada masing-masing chain dalam network. Berikut adalah ilustrasi permodelan eight-chain:

Dengan mengkombinasikan permodelan mekanika statistik, diperoleh persamaan model Arruda-Boyce sebagai berikut:
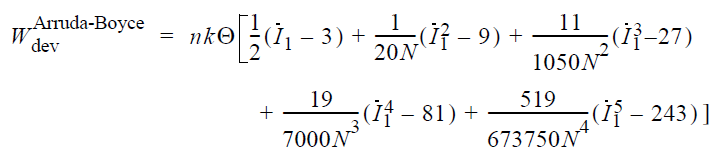
Model Gent
Dengan asumsi bahwa chain memiliki batas ekstensibilitas, Gent menawarkan bentuk persamaan sebagai berikut:

Nilai dari EI tidak tergantung dari panjang molekul dan derajat crosslingking. Model ini menjadi menarik karena sederhana namun dapat mengakomodasi ekstesibilitas molekul sampai taraf tertentu.
Foam Model
Terkadang, model elastomer menunjukkan deformasi volumetrik yang sangat ekstrim, sehingga model-model di atas tidak lagi berlaku. Sehingga digunakanlah model foam sebagai berikut:

Sampai sejauh ini, kita belum membahas best practice dari penggunaan model-model material di atas pada contoh penggunaanya. Hal ini karena memang semua adalah model eksperimental, yang koefisien-koefisienya harus dicocokkan dengan hasil curve fitting; hasil curve fitting yang paling mendekati lah yang dapat digunakan sebagai model material terbaik untuk kasus spesifik tertentu.
Berikut adalah referensi video tutorial untuk melakukan curve-fitting tersebut:
BERIKUT ADALAH REFERENSI PENGAMBILAN DATA EKSPERIMENTAL UNTUK CURVE FITTING
Untuk penggunaan desain sehari-hari, model-model material di atas dapat digunakan dan tersedia dengan lengkap pada software MSC Nastran menggunakan Implicit Nonlinear solver (SOL 400). Selengkapnya tentang MSC Nastran.
Atau untuk simulasi non-linear structure yang lebih advanced dan mendalam, anda dapat menggunakan software MSC Marc. Selengkapnya tentang MSC Marc.





