beban lokal pada pressure vessel

Tegangan yang disebabkan oleh beban lokal eksternal menjadi perhatian utama bagi desainer pressure vessel. Teknik untuk menganalisis tekanan lokal dan metode penanganannya pembebanan untuk menjaga tegangan ini dalam batas yang ditentukan telah menjadi fokus banyak penelitian. Berbagai teori dan teknik telah diusulkan dan diselidiki oleh pengujian eksperimental untuk memverifikasi keakuratan solusi.

Berikut adalah contoh-contoh beban eksternal yang umum dianalisis oleh para desainer pressure vessel:

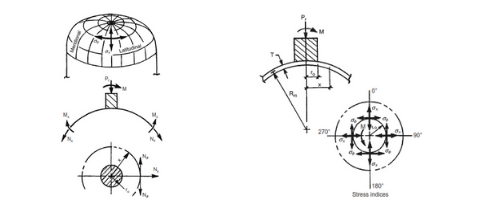
Tegangan pada cincin melingkar

Keliling cangkang sering dihubungkan dengan cincin melingkar untuk mentransmisikan gaya dan momen. Teori tegangan dan deformasi cincin adalah bagian dari teori mekanika teknik.

Beban radial

Beban per satuan panjang sumbu diasumsikan: P = P_n cos nϴ .
Tegangan resultan: N = – [(Pn α)/(n²-1)] cos nϴ ; M₂ = – [(Pn α²)/(n²-1)] cos nϴ
Displacement: v = – [(P_n α)/(n²-1)] {[(α² )/ (n²-1)EI₂ + (1/EA)]} sin nϴ ; w = [(P_n α²) / (n²-1)² EI₂] cos nϴ

Beban tangensial

Beban per satuan panjang sumbu diasumsikan P = P_n sin nϴ
Tegangan resultan: N = – [(nP_n α)/(n²-1)] cos nϴ ; M₂ = – [(P_n α²)/n(n²-1)] cos nϴ
Displacement: v = – [(P_n α²)/(n²-1)] {[(α² )/ (n²(n²-1)EI₂) + (1/EA)]} sin nϴ ; w = [(P_n α⁴) / (n²-1)² EI₂] cos nϴ

Beban Normal

Beban per satuan panjang sumbu diasumsikan P = P_n cos nϴ
Tegangan resultan: M₁ = – [(P_n α)/(n²-1)] cos nϴ ; M_T = – [(P_n α²)/n(n²-1)] sin nϴ
Defleksi: u = [(P_n α⁴)/(n²-1)²] {[1/(n²GJ_T)]+ (1/EI₁)} cos nϴ
Rotasi penampang pada bidangnya: [(P_n α³)/(n²-1)²] {[1/(GJ_T)]+ (1/EI₁)} cos nϴ

Desain Stiffeners (pengaku) Cincin Parsial

Contoh beban pada stiffeners cincin parsial

Beban Tunggal

Tentukan beban terpusat pada masing-masing pengaku tergantung pada apakah ada beban radial atau pembebanan momen, pengaku tunggal atau ganda. f=……
Kemudian menghitung konstanta kekakuan bahan (pegas) K = E_vt/R² ; Ev= modulus elastisitas cangkang, t= ketebalan, R= jari-jari.
Menentukan momen inersia dan section modulus dari stiffener misalnya bentuknya adalah persegi panjang maka rumus yang dipakai adalah I = bh³/12 dan Z = bh²/6.
Menentukan faktor damping β berdasarkan bentuk stiffener. β = [K/(4E_sI)]^1/4 ; Es = modulus elastisitas stiffener
Menentukan bending moment M = f/4β
Menentukan tegangan bending f_b = M/Z

Beban jamak

Tentukan beban terpusat pada pengaku dan beban harus sama besarnya. f= f1 = f2 = ……. = f_n
Kemudian menghitung konstanta kekakuan bahan (pegas) K = E_vt/R² ; Ev= modulus elastisitas cangkang, t= ketebalan, R= jari-jari.
Menentukan momen inersia dan section modulus dari stiffener misalnya bentuknya adalah persegi panjang maka rumus yang dipakai adalah I = bh³/12 dan Z = bh²/6.
Menentukan faktor damping β berdasarkan bentuk stiffener. β = [K/(4E_sI)]^1/4 ; Es = modulus elastisitas stiffener
Menentukan bending moment M = f/4β (ΣF_x)
Menentukan tegangan bending f_b = M/Z